直接波によるＱＳＯの理論的解説(そんなに難しくないよ)
概要
６ｍでのＱＳＯは、比較的短時間だけ生じる異常伝搬を除いては、通常は直接波でのＱＳＯが主流となります。この直接波、要は見通し範囲内だったら届くわけですが、この見通し範囲そのものが我々の考えている世界とはちょっと違います。地形が一定でも大気の悪戯で見通し範囲が日夜変動するのです。ここでは見通し範囲の詳細な考え方を紹介します。グランドウェーブによる遠距離通信では良くある、周期の長いＱＳＢの原因に深く関係しています。
単純な見通し距離の計算
まず、最初にある地点からの見通し距離（どのくらい遠くが見えるか）を単純に考えてみましょう。それには「算数」だけでは間に合わずにちょっとした「数学」の知識が必要です。多くの方は既に忘れてしまったであろう幾何の公式を思い出していただきましょう。まず、左の図をご覧下さい。丸は地球だと考えて下さい。ｒは地球の半径で、Ｃ点が標高ｈ[m]の山頂だとします。Ｃ点から見える地平線の限界地点は、Ｃ点から直線を引いて地表と接するＢ点になります。Ｃ点直下の地表面に当たるＡ点とＢ点の間の距離（弧の長さ）、つまり視界の限界を計算してみましょう。
まず、図１の三角形ＢＣＯに着目すると(1)式が成り立ちます（おお、苦手の三角関数だ）
ｒ
ＣＯＳθ＝−−−−−・・・・・（１）
ｒ＋ｈ
ここでθの単位は、以後の計算を簡単にするためにラジアンで行います
（３６０度は２πラジアンになります）。
次にラジアンの考え方を習った最初に出て来たであろう公式を思い出して下さい。
ｄ＝ｒ×θ・・・・・・・・・・（２）
角度をラジアンで表すと、（２）のように円弧の長さが直接求められますのでこの場合は便利なのです。（１）、（２）をあわせると次のような式に書き直せます。
-1 ｒ
ｄ＝ｒ×ｃｏｓ −−−−− ・・・（３）
ｒ＋ｈ
例えば標高２０００ｍの山頂からの見通し距離は（３）式にｒ＝６３７０ｋｍ，ｈ＝２ｋｍを代入すればよく、計算してみるとｄ＝１６０ｋｍとなり、２０００ｍの高さの山から海抜０ｍの平野を見おろすと１６０ｋｍ先まで見えることになります。（３）式のｈに色々な数字を入れれば、色々な高さの山からの見通し範囲が計算できます。ただし、これは途中の伝搬経路には全く障害物がないと考えた場合で、当然ながら途中に高い山があれば遮蔽されて、それより遠くは見晴らしはありません。
大気の屈折を考えた場合の見通し距離の計算
ところが、現実にはちょっと面白いことが起こります。山登りをやっている皆さんなら実感があるでしょう、地球の大気は上空ほど薄くなります。空気の密度が一定ですと空気の屈折率も一定ですので光は直進しますが、このように密度が変化すると僅かですが屈折します。上下どちらに屈折するかというと、無線屋にはちょうど良い？ことに下に向かってくれます。この解釈を変えて、電波は直進したことにして地球の半径を大きめにとってやることもできます。これなら光は直進したことにできるので何かと計算が楽になります。この時の地球の半径を、その筋では「等価地球半径」と呼びます。
それでは、どのくらい地球が大きくなったのと同じ効果が得られるのでしょうか。標準的な大気の状態では、元の地球の半径よりも４／３倍、つまり１．３倍大きくなっています。意外と大きいですね。半径が大きくなるということは、丸みが緩くなって同じ高さの山でももっと遠くが見えることを意味します。では、どのくらい遠くが見えるようになるかと言うと、地球の半径が１．３倍大きくなったのと同じですから、（３）式のｒの値を１．３倍して計算すればいいわけです。計算してみると標高２０００ｍの山では１８４ｋｍまで見えるようになります。もとの計算よりも２４ｋｍ延びていますね。
「等価地球半径」は一定ではない
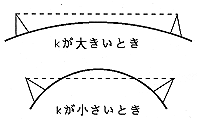まだおまけが続きます。「等価地球半径は実際の地球半径の４／３倍である」のは大気が「標準状態」であるときです。しかし現実には高気圧、低気圧が存在したり、大気の温度分布に変化があったり、湿度も異なったりして４／３であるとは限りません。また、時間的にも一定ではなく、常に変化しています。等化半径が大きくなると地面の丸みが小さくなって平面に近くなりますから、同じ高さでも見通し距離が延びます。逆に等価半径が小さくなると見通し距離が狭くなってしまいます。そう考えると、見通し距離は等価地球半径の変化にともなって陽炎のようにユラユラと変動しているはずです。ＱＳＯ相手の距離が近くて、等価半径が少しくらい変動してもその見通し範囲内に入っている時にはＱＳＢはありません。ところが、距離が遠くなって標準状態でも見通し距離ぎりぎりくらいの相手局になると、少しでも等価半径が小さくなると見通し距離からはずれてしまい、電波が地表面に遮蔽されて受信ﾚﾍﾞﾙが低下します。つまりＱＳＢを生じます。
さて、今までの経験では１日の内で最もグランドウェーブが延びる時間は朝方です。夕方も延びますが、今までの経験では朝方の飛びには全然かないません。これも等価半径の考え方で説明できます。等価半径の考え方が成り立つのは地球の重力による空気密度の変化だけではありません。要は高度が低いほど空気の密度が高ければいいわけですから、例えば地表面ほど気温が低くなっても、地表面ほど水蒸気量が多くてもその条件を満たすはずです。地表面の空気が冷やされるといえば、晴れた日の朝に生じる「放射冷却」が代表格です。そうです、これが朝方グランドウェーブが延びる原因です。真っ昼間になると太陽光により地表面が熱せられ、暖められた地面によって地表付近の空気が暖められられ、気温が上昇します。つまり、日光が当たっている昼間だと、地表ほど気温が高くなって等価半径が小さくなってしまいます。どうでしょう、経験則と合っていますね。ただし、いくら朝方でも風が強いと空気が撹拌されて温度分布は均一となって、等価半径の増大は期待できないでしょう。
また、短い時間の変動だけでなく、もっと長期的に見てみると季節による等価半径の変化の傾向も認められます。統計的には夏の方が等価半径の値が大きく、最大で通常時の１０倍にもなることがあるそうですので、冬よりも遠くまで届くことになります。ただ、夏は値の変動が激しく、そのような異常な状態は長時間は続かないようです。
結論
こう考えてみると、「等価半径」の考え方は６ｍの実際の伝搬と合致することが多いことに気づくでしょう。
・近距離のＱＳＯではＱＳＢはない。
・遠距離のＱＳＯほどＱＳＢがある。
・冬よりも夏の方がグランドウェーブが延びる。
・朝方が１日の中で最もグランドウェーブが延びる。
どうやら、この理論は信頼できそうです。事実、このような「等価地球半径の変動による見通し範囲の変化」は、マイクロ波の回線設計を行う場合は考慮に入れ、ある程度等価半径が小さくなっても見通し距離から外れないような場所に中継局を置いています。なお、等価地球半径の変動によるＱＳＢのことを、専門用語では「ｋ形フェージング」（ｋとは等価地球半径のこと）と呼んでいます。
最後に
どうですか、参考になったでしょう？ これからは伝搬路上が晴れた早朝は、早起きしてじっくりワッチしましょう。きっといつもよりも強力に遠くの局が聞こえてくるでしょう。これこそ「早起きは３文の得」です。
DE JS1MLQ NIFTY:MXL02562 小金井市 川田
